Перед чтением этого приложения мы рекомендуем просмотреть еще раз §2 Гл.1 (первый раздел) Части 2.

Во-первых, здесь Соловьев использует три начала-степени, и они предполагаются линейно упорядоченными. Оформим эти отношения в следующем виде (см рис.45).

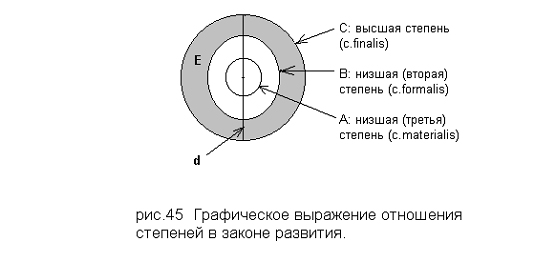
На рис.45 круг А включен в В, который включен в круг С. Такое отношение можно оправдать неоднократным упоминанием Соловьева о подчинении низших степеней высшим. Предположим далее возможность представления в качестве модусов всех элементов –

А, В, С, Е=С\В и нулевого элемента 0 – в рамках некоторого ментального многообразия со всеединством. Модус, сопоставленный элементу Х, будем обозначать через M_Х. Вооружившись этими средствами, вернемся к трактовке моментов развития у Соловьева.

1-й момент развития: состояние безразличного смешения степеней можно трактовать как данность всех модусов начал: M_А, M_В и M_С в модах Х↓M⁰, т.е. в собственной модели нулевого модуса. Это приводит к “смешению” модусов, их неразличимости, т.к. M_Х↓M⁰ – это ноль булевой алгебры в модели mM⁰ при любом Х. Итак, степени А, В и С мы интерпретируем как модусы M_А, M_В, M_С соотв., и в первом моменте развития они представлены своими нулевыми модами: M_А↓M⁰, M_В↓M⁰ и M_С↓M⁰. Эти же моды можно трактовать как потенциальное бытие соответствующих модусов. Соловьев отмечает относительность неразличимости (“безразличия”) степеней в 1-м моменте: с некоторой точки зрения здесь есть “зародышная организация”, которая сохраняет отношение (порядок) начал, но в умалённом виде (I, т.2,С.154). Мы можем выразить это в нашей модели, если нулевой элемент 0 будем интерпретировать как множество на плоскости с нулевой площадью. Например, это может быть какой-нибудь отрезок, пересечения с которым областей А, В, С сохраняют отношения этих областей. Рассечем круг С диаметром d (см. рис.45) и построим нулевой модус над d: M⁰=M_d. Тогда моде M_С↓M_d соответствует множество С∩d=d, M_B↓M_d – диаметр В (b), M_А↓M_d – диаметр А (а). Т.о. в первичном состоянии смешения отношение кругов дано как отношение их диаметров, которые “безразличны” с точки зрения кругов, т.е. все есть одинаково нули как площади. В модели mM⁰ как mM_d поглощение высшей степенью низших степеней (условие 2) и условие 3 – растворение в низших степенях высшей – можно трактовать как две стороны одной неразличимости: a,b, с одной стороны, и d, с другой, – с точки зрения меры площади.

2-й момент развития:

2.1-й момент: 1)высвобождение низших степеней из-под власти высшей можно интерпретировать как переход в модель модуса M_Х, где Х=А∪В – слиянное единство низших степеней, противостоящее свободе высшей степени. Т.к. в нашем случае А∪В=В, т.е. А подчинено В, то “вторая степень, еще включая в себя третью, отделяется от первой”. Т.о. мы переходим в модель модуса M_В. 2)одновременно высшая степень отделяется от низших и обретает свою свободу, которая в последующем заложит основу для свободного синтеза, т.е. С уже не будет исчерпываться А∪В. Высшая степень в этом моменте развития дана в модели модуса M_Е, т.к. Е=С\(А∪В).

Итак, 2.1-й момент – это образование двух моделей: mM_B и mM_E. В первой из них низшие степени находят свое слиянное единство в лице 2-й степени и одинаково в нем противостоят свободе высшей степени. В модели mM_E высшая степень обретает свою свободу от низших степеней, т.е. высшая степень как модус M_С дана в этой модели в виде моды M_С↓M_Е.

2.2-й момент: побеждает в реальности модель низших степеней, т.е. mM_B. Модель mM_E подавляется и потенциализируется.

2.2.1-й момент: происходит утверждение себя со стороны второй степени. Т.к. в нашем случае А∪В=В, то 2.2.1-й момент совпадает с 2.2-м моментом (с другой стороны, если все же Соловьев отличает 2.2.1-й момент от 2.2-го, то тем самым предполагается, что в отношениях низших степеней есть элемент рядоположенности, в связи с которым А∪В≠В, и момент 2.2.1 отделяется от момента 2.2.).

2.2.2-й момент: утверждает себя третья степень, т.е. происходит переход к модели модуса M_А, где этот модус дан в виде рефлексивной моды M_А↓M_А.

3-й момент: этот момент можно трактовать как: 1)соединение в высшей степени единства своей свободы от низших степеней (моды M_С↓M_Е) и включения их в себя (моды M_С↓M_В), т.е. как вхождение в синтетическую модель mM_Cи завершение полноты модуса M_С, 2) кроме того, в этом моменте развития все начала собирают в своем бытии все свои моды, и 3-й момент можно также трактовать как выход из условий модельности вообще, обретение началами статусов полных модусов – как единства всех своих мод, не сводимых ни к ним самим, ни к их частичным совокупностям (в связи с чем стоит заметить, что даже в рамках своего утопизма Соловьев всегда понимал свободную теократию трансрационально и описывал ее в терминах реальности “не от мира сего”).

Итак, третий момент – это собирание всей полноты ментального многообразия, всех его модусов, и в этом процессе достижение модели максимального модуса носит лишь “пусковой” характер.