Мы неоднократно отмечали модальный характер логики всеединства. Сущее, как источник предикации, выражает себя в различного рода отношениях в форме предикатов. Отрываясь от терминологии Соловьева и придавая этим конструкциям логическое звучание, мы стали употреблять термины “модус” для сущего (сущих) и “мода” для его предикатов. Итак, модус и мода. Модус в различных отношениях выражает себя в виде своих мод. Порождая моды, модусы относятся между собой, но во всяком модальном отношении есть асимметрия: существует модус активный, выражающий себя в виде моды, и модус пассивный, обеспечивающий условия проявления первого модуса в форме именно такой моды. Термином “модус” мы отмечаем в большей мере активный источник предикации, обозначая страдательные условия проявления второго модуса в термине “модель”. Итак, мода А↓В – “А при условии В” – порождается отношением модуса А к модусу В, что означает образование моды модуса А в собственной модели модуса В. Т.о. каждому модусу сопоставляется его собственная модель – как условие наиболее адекватного и полного выражения модуса в модах. Например, теоретическую деятельность можно рассмотреть в своей собственной модели, как это сделано в “Началах” Соловьева, а можно представить в модели практической деятельности, как это было осуществлено Соловьевым в “Оправдании добра”. Каждое начало может выражаться множеством своих мод: знание на своей собственной почве (модели), знание на почве воли, на почве чувства; аналогично, чувство можно рассмотреть на своей собственной почве, на почве воли, на почве знания. Получается, что каждое начало – это нечто большее, чем то или иное его представление при каких-либо условиях. Начало – это модус, и оно может выражаться во множестве своих мод в отношениях к другим началам-модусам. Вот основания модальности в логике всеединства, не раз подчеркиваемые нами в логике абсолютного и критике отвлеченных начал у Соловьева, Флоренского и др. В принятых нами логических терминах это выглядит так: есть множество модусов, и для любых двух модусов А и В можно образовать моды А↓В – “А при условии В” и В↓А – “В при условии А”. В том числе, возможен случай, когда А=В, тогда образуется одна мода А↓А – “А при условии самого себя” (в своей собственной модели). Моду А↓А мы называли рефлексивной, все остальные моды А↓В, где А≠В, – трансфлексивными, особенно выделяя в ней тот случай, где В в каком-либо отношении отрицает А.
Заметим, что в моде А↓В элемент слева от стрелки (А) обозначает тот модус, в состав которого входит обозначенная мода (который выражает себя в ней), элемент справа от стрелки (В) обозначает тот модус, в собственной модели которого (т.е. при тех условиях, которые наиболее благоприятны для модального выражения этого модуса) образуется указанная мода.
Какие требования следует предъявить к множеству модусов и их мод?
Модусы – это логические эквиваленты начал, и в “Критике отвлеченных начал” Соловьева мы видели, что множество начал образует иерархию, т.е. на нем задано отношение порядка, хотя возможен и случай несравнимых начал.
Итак, на множестве модусов могут быть заданы отношения порядка и равенства.
Кроме того, выше мы отмечали, что в собственной модели модуса его мода оказывается доминирующей, моды всех остальных модусов либо подчиняются ей, либо совпадают с ней (что, впрочем, тоже можно рассмотреть как частный случай подчинения). Т.о. на множестве мод также заданы отношения порядка и равенства.
Оформим эти идеи немного более строго.
Пусть < – отношение порядка (“меньше”) с известными в математике свойствами (нерефлексивности, несимметричности и транзитивности). Предполагаем, что отношение порядка и равенства (=) заданы на множествах мод и модусов, хотя, возможно, порядок задан не для всех пар элементов (частичный порядок).
Тогда, во-первых, если мы находимся при условиях собственной модели некоторого модуса, например, модуса В, то примем здесь следующее свойство:
О1. Для любого модуса Х верно: Х↓В £ В↓В,
т.е. мода любого модуса в модели В подчинена рефлексивной моде модуса В (заметим, что условия нахождения модуса Х в модели В выражаются в том, что модус Х берется как мода Х↓В – “Х при условии В”). Свойство О1 выражает требование аксиомы неэлиминируемости (АН) того, чтобы во всякой модели (как реальном всеединстве) всегда было доминирующее начало (см. Часть 2, Гл.1, Раздел2, §1).
Далее возникает проблема, как соотносятся между собою системы отношений на модусах и модах. Аксиома равносильности (АР) выражает требование высокой однозначности между топосом модуса, его местом в системе модусных отношений, и системой отношений на модах в собственной модели данного модуса.
Пусть между модусами А и В задано отношение R(А,В), каково в этом случае будет отношение R’(А↓С, В↓С) между модами этих модусов в модели модуса С?
Мы не будем пытаться решать эту проблему однозначно, предполагая, что здесь возможно не единственное решение. Все эти решения (в рамках выражения идей философской логики в русской философии всеединства) должны лишь удовлетворять требованию О1.
Мы ограничимся пока примером одного из возможных решений, считая его вполне показательным в системе всех возможных решений.
Рассмотрим достаточно несложный пример системы отношений областей на плоскости, изображенный на рис.40.
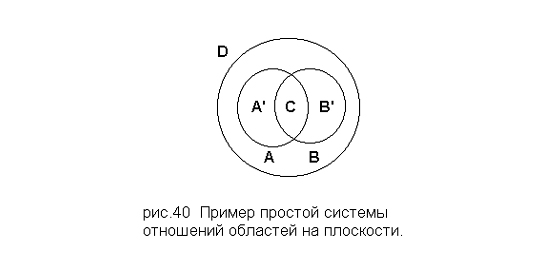
Здесь изображены шесть элементов: А, А’, В, В’, С и D. Зададим на них отношение порядка, считая, что X<Y, если область X строго включена в область Y. Равенство определено как совпадение областей.
Поставим в соответствие моде X↓Y пересечение областей X и Y, например: А↓В соответствует С, как и В↓А. Чтобы отличить моды А↓В и В↓А, введем здесь еще одно требование: пусть условие X↓Y означает, что область, соответствующая Y, растягивается до размеров области D. В этом случае мы будем иметь следующие варианты для моделей модусов А и В (рис.41).
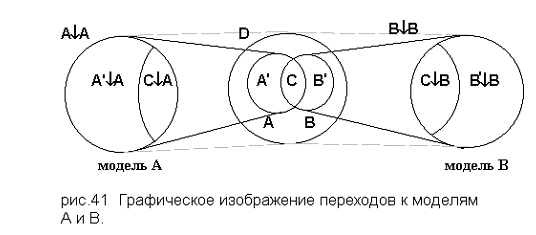
Пока будем отождествлять моды и сопоставленные им области.
Здесь (см. рис.41) А↓В = С↓В и В↓А = С↓А, и эти пары мод не совпадают друг с другом, т.к. относятся к разным моделям. Т.о. требования к равенству пока таковы: моды равны, если им сопоставлена одна область в одной модели.
Заметим, что первоначальный рис.40 – тоже одна из моделей, а именно собственная модель D, и все области в ней даны как моды X↓D. Эта модель имеет одну особенность – в ней “видны” все элементы, в то время как в других моделях часть элементов может оказываться неразличимой (например, B’↓A или A’↓B). Модель D – это модель самого “крупного” элемента. Но что это значит, почему элемент D самый “крупный”? Во-первых, он включает в себя все иные элементы в своей собственной модели. Во-вторых, если мы возьмем любой элемент Х и образуем его модель, то в ней все моды будут подчинены моде Х↓Х, а мода D↓Х будет равна этой моде, т.к. пересечение D с Х
равно Х. Получается, что элемент D самый “крупный” потому, что для любых элементов X и Y: X↓Y £ D↓Y,т.е. мода D в любой модели совпадает с доминирующей (максимальной) модой (Y↓Y) в этой модели. Теперь мы могли бы взять и это свойство в качестве общего определения максимального элемента. Далее мы везде предполагаем, что на множестве элементов (модусов – см. ниже) определен максимальный элемент.
Итак, начав с одной системы отношений на рис.40, мы можем образовать множество систем отношений, каждую из них назвав “моделью” соответствующего элемента. Элементу Х сопоставляется множество областей X↓Y, каждую из которых мы называем “модой”. Модусом Х назовем теперь множество всех мод вида X↓Y, где Y пробегает все имеющиеся элементы, т.е. Х-модус – это все Х-моды, полученные во всех моделях. Например, модус А – это множество мод А↓А, А↓В, А↓С, А↓А’, А↓В’, А↓D. Заметим, что модус А – это уже не элемент А на рис.40, но этот последний – одна из его мод (A↓D).
Модель (собственная) модуса Х – это множество всех мод вида Y↓X, где Y пробегает по всем элементам. Например, модель А – это множество мод А↓А, В↓А, С↓А, А’↓А, В’↓А, D↓A (изображена на рис.41 слева). Все эти определения (главным образом, это относится к моде) будут ниже уточнены нами, но пока для наших целей достаточно и уже введенных пояснений.
Собственную модель модуса Х будем обозначать через mХ, полагая, что:
Х↓Y = Х↓mY ,
т.е. мода “Х при условии Y” означает “Х при условии модели Y”.
Модель Х можно трактовать как некоторое условие абсолютизации модуса Х, сообщающее возможность доминирования этого модуса и определяющее его проявления в рефлексивной моде.
Мы ввели для интерпретации модальных отношений в логике всеединства достаточно несложные средства, использующие графическую интерпретацию. Особенность этого случая состоит в том, что здесь, кроме свойства О1, выполнены соотношения:
О2. Если X £ Y, то X↓Z £ Y↓Z – для любых модусов X, Y, Z.
О3. Если X < Y, то Y↓X = X↓X (здесь имеется в виду равенство в рамках модели Х).
Свойство О2 выражает достаточно большую степень сохранности модусных отношений в отношениях мод. Здесь отклонение возможно в случае, если Х < Y, но X↓Z = Y↓Z.
Свойство О3 выражает описанный в “Критике отвлечённых начал” феномен экранизации высшего начала низшим при доминировании последнего.
Выбранный нами случай модальных отношений на геометрических областях отвечает аксиоме равносильности и вообще всем аксиомам АН, АЭ и АР, выявленным нами в критике начал в философии всеединства. Ниже мы будем активно привлекать этот случай для иллюстраций общих понятий логики всеединства.
При образовании модели той или иной области, она растягивается до размеров области D. Точнее это выражается так: в модели модуса Х мода Х↓Х выражается размерами моды D↓D. Эти размеры задают как бы экран, в рамках которого происходит тотализация (растягивание) рефлексивных мод доминирующих модусов.
Будем говорить, что:
– модус Х дан в L-статусе в модели модуса Y, если X↓Y = Y↓Y, и моду X↓Y в этом случае обозначим как X↓L – “X дан в L-статусе”.
– Модус X дан в M-статусе в модели модуса Y, если X↓Y < Y↓Y, и моду X↓Y в этом случае обозначим как X↓M – “X в M-статусе”.
Будем говорить, что модус X определен в собственном L-статусе, если он дан в рефлексивной моде Х↓Х, и обозначим этот случай в виде X↓OL (“own L-status”). Все прочие L-статусы X можно называть несобственными.
Например, в случае геометрической интерпретации (назовем ее R2 – многообразием, где R2 – вещественная плоскость) имеем: А↓В = А↓M , А↓D = А↓M , D↓А = D↓L и т.д.
Т.к. X↓Y £ Y↓Y для любых модусов X и Y (см. О1), то случаи L– и M-статусов исчерпывают весь спектр возможностей. Любой модус в любой модели находится либо в M-, либо в L-статусе.
Переход между статусами одного модуса назовем R-преобразованиями. В общем случае возможны 4 вида R-преобразований (рис.42).
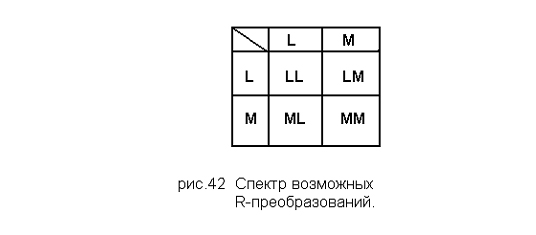
Если a и b – некоторые статусы, то может быть определено ab-преобразование, например LM-преобразование.
L– и M-статусы будем объединять под общим термином R-статусов.
Уточнение и развитие введенных понятий мы продолжим ниже.
