В общем случае голоморфность мы понимаем как свойство части содержать в себе дополнение до целого в некотором непроявленном виде. Эта идея может быть, по-видимому, реализована разными способами. Ниже мы приводим в качестве иллюстрации один из возможных (топологических) способов выражения голоморфности.

Предположим далее, что для множества мод каждой модели в ментальном многообразии задана топология, т.е. можно ввести открытые множества, их границы, замыкания открытых множеств и т.д. Допустим, что каждой моде X↓Y в модели Y можно поставить в соответствие открытое множество – внутренность моды X↓Y: IntX↓Y.

В случае R²-многообразия мода выражается двумерной областью, внутренность моды будем интерпретировать как внутренность области в обычной топологии на R², т.е. как область без границы. 

Чтобы теснее связать моды и их внутренности, примем, что:

1. На модах одной модели заданы булевы операции пересечения (∩) и объединения(∪), которые согласованы с отношением порядка:  X↓Z < Y↓Z означает, что X↓Z ∩Y↓Z = X↓Z и X↓Z ∪ Y↓Z = Y↓Z, причем X↓Z ≠ Y↓Z. Можно сказать и так, что множество мод на каждой модели образует решетку.

2. Для множества внутренностей мод очевидным образом определены булевы операции пересечения и объединения, т.е. это множество тоже образует решетку. Мы принимаем, что решетки мод и их внутренностей изоморфны, т.е.

(I1)    Int(X↓Z * Y↓Z) = IntX↓Z * IntY↓Z ,

где * – операция пересечения (∩) или объединения (∪).

Будем предполагать, что решетка на модах всегда может быть дополнена до булевой алгебры, т.е. операции пересечения (∩) и объединения (∪) могут быть восполнены операцией дополнения (⌉), и получающаяся введением новых элементов булева алгебра будет минимальной из всех возможных булевых алгебр, достраиваемых над решеткой мод. Ей соответствует изоморфная булева алгебра множеств из топологии, сопоставленной модели.

Мы рассматриваем случаи ментальных многообразий с максимальным модусом M¹, т.е. M ≤ M¹ для любого модуса M. Кроме того, для моделирования логики всеединства мы принимаем свойства О1-О3. Свойства нестрогого порядка на модусах в этом случае вполне переносятся на множества мод. В то же время множество мод в рамках каждой модели определено как решетка. Мы предполагаем, что эти решеточные свойства также переносятся на моды с множества модусов, последнее тоже определено как решетка, т.е. на нем заданы операции пересечения (∩) и объединения (∪), и существует изоморфизм вида:

(I2)     (M₁ * M₂ )↓M₃  = M₁↓M₃  *  M₂↓M₃,

       где M₁, M₂, M₃ – любые три модуса,

       * – операции пересечения (∩) или объединения (∪).

Предположим также возможность пополнения решетки модусов до минимальной булевой алгебры, где:

(I3)      (⌉M)↓M’  =  ⌉(M↓M’).

Для случая R² -многообразия мы теперь хотели бы ввести то уточнение, что мода А↓В – это не совсем соответствующая ей область на диаграммах, хотя в плане порядка, пересечения и объединения моды и их внутренности вполне эквивалентны, что и позволило нам в предыдущем параграфе говорить о модах в терминах сопоставленных им областей на плоскости.

Итак, что же еще мы вкладываем в понятие “моды”, кроме соответствующей ей внутренности?

Теперь моду А↓B в топологическом плане будем понимать как замкнутое множество IntА↓B ∪ ∂IntА↓B – внутренность моды вместе с ее границей, причем, предположим, что существует отображение “свёртки” Р_B(⌉Int((А ∩ B)↓M¹)) = ∂IntА↓B, сопоставляющее дополнению от Int((А ∩ B)↓M¹)до IntM¹↓M¹ границу ∂IntА↓B, как бы сворачивающее это дополнение в границу.

На рис.43 мы изображаем эти объекты для моды в R²-многообразии – см. рис.43 (в R²-многообразии M¹  – это D, и на рис.43 замыкание множества Int((D\(А∩В))↓D) обозначено через ⌉Int((А∩В)↓D)).

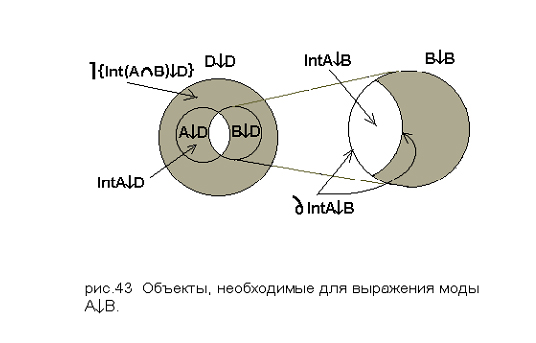
 Мода A↓B – это в усовершенном виде мода M¹↓M¹, т.е. рефлексивная мода максимального модуса. В нашем случае M¹ = D, и всякая мода – это в усовершении мода D↓D. Но мода M¹↓M¹ дана в A↓B в “умалении”, а именно:

Р_B(Int(M¹↓M¹)) =  Р_B((⌉Int((A∩B)↓M¹) ∪ (Int((A∩B)↓M¹))) =

Р_B(⌉Int((A∩B)↓M¹)) ∪ Р_B(Int((A∩B)↓M¹)) = ∂IntA↓B ∪ IntA↓B,

т.е. можно положить, что:

Р_B(⌉Int((A∩B)↓M¹)) = ∂IntA↓B,

Р_B(Int((A∩B)↓M¹)) = IntA↓B.

Т.о. IntM¹↓M¹ разбивается на две дополнительные части, одна из которых (⌉Int((A∩B)↓M¹)) сворачивается в границу моды A↓B, а другая (Int((A∩B)↓M¹)) представляется внутренностью этой моды. Если Р_B(Int((A∩B)↓M¹)) = IntA↓B – гомеоморфизм, то адекватное представление IntM¹↓M¹ в моде A↓B достигается лишь в меру внутренности моды (A∩B)↓M¹, вся оставшаяся часть IntM¹↓M¹ «стяжённо» присутствует в моде A↓B в виде ее границы.

Т.о. в топологическом плане любая мода A↓B – это всегда мода M¹↓M¹ в своем умалении и стяжении – так обеспечивается голоморфность мод. Топологию, выражающую идею голоморфности в рамках того или иного ментального многообразия, можно было бы называть «ментальной топологией».